Nel seguente paragrafo si espongono delle considerazioni sul comportamento della membratura in condizioni d’incendio, oltre che sul loro comportamento plastico delle stesse. Negli esempi, si considerano gli elementi che si trovano all’interno della struttura da prendere in esame nella sua totalità, applicando dei metodi avanzati.
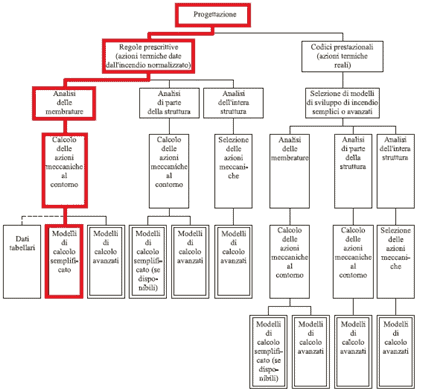
Per determinare dei fenomeni fondamentali, che si possono osservare su di una struttura durante l’incendio, si sono fissati dei principi molto importanti per comprendere le complesse interazioni fra i vari meccanismi strutturali che avvengono. Tali fondamenti sono utili per analizzare ed interpretare i risultati che si possono ottenere per mezzo dei metodi di analisi più sofisticati e sviluppati.
La principale relazione, che determina il comportamento delle strutture che subiscono effetti termici, è:
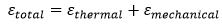
La deformata strutturale (ε_tot->delta ) è influenzata dalle deformazioni nel loro complesso, per mezzo di relazioni di congruenza oppure cinematiche. Al contrario, lo stato tensionale nella struttura (ε_mecc->sigma ), sia esso plastico che elastico, è governato dalle deformazioni meccaniche. Nel momento in cui non vi è l’applicazione di carichi esterni e non vi è la presenza di vincoli capaci di limitare le deformazioni termiche, allora si verifica un annullamento delle deformazioni meccaniche (ε_mecc=0 ), dunque:
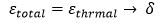
Nel momento in cui, invece, i vincoli presenti non permettono alle deformazioni termiche uno sviluppo in mancanza di carichi esterni, le deformazioni totali sono pari a zero (ε_tot=0 ), perciò:
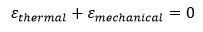
In aggiunta al decadimento termico di cui sono vittima i materiali, un altro fattore estremamente importante, determinante per la reale risposta di una struttura durante l’incendio, è il modo con cui la struttura fa fronte alle deformazioni termiche, conseguenti all’aumento delle temperature all’interno dei suoi elementi. Quando la struttura non possiede vincoli d’estremità per opporsi alle deformazioni di tipo termico, la risposta sarà fissata dagli spostamenti, al contrario si avranno dei rilevanti stati tensionali. Considerando una trave esposta ad un incendio dal basso, ad esempio, essa aumenta la propria temperatura, presentando un dato gradiente di temperatura sulla sezione retta, il quale può approssimarsi per semplicità attraverso una legge lineare e dividersi in una distribuzione costante delle temperature sulla totalità della sezione e in una distribuzione di tipo bi-triangolare. La prima crea nell’elemento strutturale, considerato di materiale omogeneo, in mancanza di vincoli alla traslazione, delle dilatazioni termiche di tipo uniforme, senza che si effettui alcuna modifica dello stato delle sollecitazioni, il cui collasso è dato dal decadimento termo-meccanico dei materiali.
Per quanto riguarda i vincoli traslazionali, essi portano all’insorgere di alcune deformazioni meccaniche uguali ed opposte rispetto a quelle termiche: si creano degli importanti stati tensionali di compressione. La parte lineare, appartenente al diagramma della temperatura, crea una serie di curvature termiche nell’elemento e, dunque, un’inflessione, la quale, dinanzi a dei vincoli alla traslazione orizzontale e nel caso di rilevanti spostamenti, inducono ad un probabile “effetto catena”, provocando uno stato tensionale di trazione. Se vi sono dei vincoli alla rotazione, le curvature termiche portano a dei momenti flettenti negativi all’interno dell’elemento.
Le risposte strutturali dipendono dallo schema statico e sono inerenti all’eventualità di presentare diversi scenari d’incendio che possono avvenire in una struttura. Un incendio del tipo “fast-burning”, capace di raggiungere velocemente il flash over e di registrare le alte temperature per poi esaurirsi, comporta elevati gradienti termici (calcestruzzo a temperature relativamente basse ed acciaio molto caldo) e dei bassi valori medi delle temperature. Un incendio lento, invece, registra solo delle temperature abbastanza modeste, ma continua nella sua combustione per un lungo lasso di tempo: in tal modo potrebbero verificarsi degli alti valori medi della temperatura e gradienti termici abbastanza bassi.
Quando una struttura reale subisce un incendio, allora vi è una combinazione di deformazioni meccaniche, causate sia dalle dilatazioni termiche non permesse, sia dai carichi che sono stati applicati. L’insieme di questi fattori comporta il superamento dei limiti di snervamento dei materiali, causando delle plasticizzazioni molto estese. La deformata della struttura, invece, è legata solo alle deformazioni nel loro complesso, che possono considerarsi piccole se presente un adeguato livello di vincolo, ma sono in grado di creare grandi deflessioni, aventi un’inferiore domanda di deformazioni plastiche, in presenza di deformazioni plastiche estese o di uno basso livello di vincolo. Tali deduzioni evidenziano come la risposta strutturale sia complessa durante l’incendio e come non sia sempre esaminabile con le classiche metodologie di calcolo a freddo “a freddo”.
I concetti sopra riportati saranno approfonditi per una maggiore precisione e chiarezza, tenendo conto delle configurazioni strutturali semplici ed applicando delle espressioni analitiche per gli eventi di grande riguardo.
Dilatazione termica in elementi isostatici
L’aumento delle temperature comporta una dilatazione termica dei materiali strutturali εT e, dunque, dei medesimi elementi. Questi due fattori possono ricavarsi con:
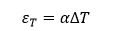
Se viene applicato un aumento uniforme della temperatura ΔT ad una trave che risulta solo appoggiata e senza dei vincoli assiali, si otterrà una dilatazione della trave uguale a:
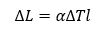
Dal momento che la deformazione totale εt equivale alla deformazione termica e che le deformazioni di tipo meccanico sono uguali a zero, non è sviluppato alcun tipo di stato tensionale.

Dilatazione termica in presenza di vincoli rigidi alla traslazione
Ora si prenda in considera una trave vincolata in maniera rigida alla traslazione e che subisce un aumento uniforme delle temperature ΔT.

Nel caso in esame la trave non può ovviamente allungarsi, dunque si avrà una deformazione totale εT pari a zero, evidenziando una mancanza di spostamenti. Si sviluppa, comunque, una reazione di vincolo P, che origina sulla trave una deformazione uguale e contraria alla deformazione di tipo termico, dunque di compressione, come evidenziato da:
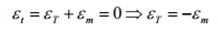
E’ presente, quindi, un regime uniforme di tensioni di tipo assiale all’interno della trave, pari a:
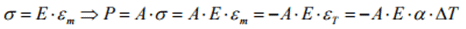
Presumendo un aumento indefinito della temperatura, è possibile che si verifichino due risposte strutturali conseguentemente alla snellezza della trave:
- Con una trave abbastanza tozza, la tensione superficiale eguaglia la tensione di snervamento del materiale e, se il materiale presenta un legame costitutivo tensione deformazione del tipo elasto-plastico, la trave snerva senza altri aumenti della tensione, ma sarà capace di immagazzinare maggiori incrementi delle deformazioni plastiche. L’aumento della temperatura che porta allo snervamento ΔT* si definisce come segue, una volta che si è posto
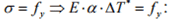
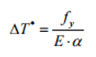
In cui:
- E indica il modulo di elasticità appartenente al materiale;
- fy si riferisce alla tensione di snervamento del materiale;
- α è il coefficiente di dilatazione termica.
- Una trave snella, d’altro canto, diventa subito instabile ancor prima del raggiungimento della tensione di snervamento. Il carico critico di Eulero per una colonna o una tre è pari a:
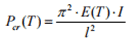
Eguagliando l’espressione della reazione vincolare si ha:
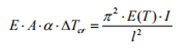
La quale porta ad un valore critico dell’aumento della temperatura, in relazione all’instabilità, equivalente a:
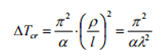
Dove:
- l lunghezza libera d’inflessione, che dipende dalle condizioni di vincolo;
- λ è il rapporto di snellezza;
- ρ raggio di inerzia.
Se si dovesse verificare un continuo aumento della temperatura, la reazione vincolare nel suo complesso rimarrà costante, se si considera un materiale elastico senza alcun tipo di decadimento termico, invece, le deformazioni termiche indurranno un incremento dell’inflessione della trave δ.

I due eventi sopra descritti rappresentano le principali tipologie di risposta delle travi soggette alla dilatazione termica e vincolate assialmente. Ognuna delle due può avere luogo in base alla snellezza della trave o alla combinazione fra instabilità e snervamento.
Dilatazione termica in presenza di vincoli laterali deformabili
Le travi, ovviamente, non sono libere di allungarsi, come avviene nel caso della trave isostatica, così come non sono del tutto vincolate, come dimostra il precedente caso, il quale mostra un limite superiore impossibile da registrare: un caso più reale, infatti, avrebbe una considerazione finita dei vincoli di rigidezza.
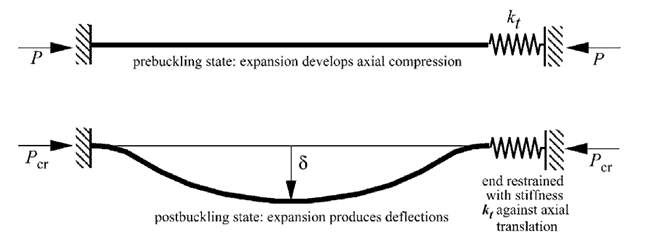
Nella figura si può osservare una trave vincolata assialmente per mezzo di molle traslazionali, aventi una rigidezza kt. La tensione assiale di compressione, che si sviluppa per mezzo della dilatazione termica, è uguale a:
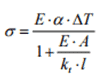
Mentre la temperatura critica di buckling è espressa come:
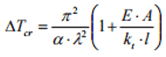
Tale equazione mostra come gli eventi di buckling e ad esso successivi si presentino a temperature attorno ai 300° C nelle strutture aventi vincoli assiali di rigidezza confrontabili alla rigidezza assiale del medesimo elemento (EA/ l).
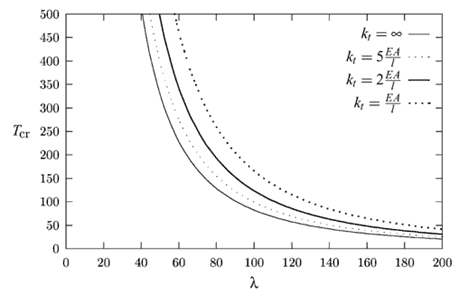
Il grafico in figura deriva dall’equazione espressa in precedenza, per cui le temperature critiche di buckling sono illustrate con riferimento alla snellezza per i diversi valori della rigidezza del vincolo. Si evidenzia come il livello di vincolo necessario per giungere alla temperatura di buckling non sia molto alto per le sezioni snelle. Considerando che la rigidezza di tipo assiale dell’elemento risulta ridotta per l’aumento delle temperature con la diminuzione del modulo di elasticità, è probabile che negli incendi reali si evidenzino tali eventi di post-buckling all’interno delle travi.



